Lesson 05: Combination Logic Circuits
5.1 Analysis of Combinational Circuits
Definition of Combinational Circuits
- Combinational circuits are digital circuits where the output at any given time depends only on the current combination of input values.
\(output = F(inputs)\) - These circuits have no memory or feedback; the output is solely determined by the current input values.

Figure 1: Block Diagram of Combinational Circuit
Basic Components of Combinational Circuits
- Logic Gates: Combinational circuits are constructed using basic logic gates such as AND, OR, NOT, NAND, NOR, XOR, and XNOR gates.
- Boolean Functions: The behavior of combinational circuits is described using Boolean functions, which express the relationship between inputs and outputs.
Design Process of Combinational Circuits
- Specification: Clearly define the inputs and outputs of the circuit and the desired behavior.
- Truth Table: Construct a truth table that lists all possible input combinations and their corresponding output values.
- Boolean Expression: Derive Boolean expressions for each output based on the truth table.
- Logic Diagram: Use the Boolean expressions to create a logic diagram consisting of interconnected logic gates.
- Verification: Simulate the circuit to ensure that it produces the correct output for all input combinations.
Examples of Combinational Circuits
- Adders: Combinational circuits that perform the addition of binary numbers.
- Subtractors: Circuits that perform subtraction by adding the two's complement of the subtrahend to the minuend.
- Multiplexers (MUX): Circuits that select one of several input data lines and direct it to the output.
- Demultiplexers (DEMUX): Circuits that take a single input and direct it to one of several output lines.
- Encoders and Decoders: Circuits that convert between different data formats, such as binary and Gray code.
- Comparators: Circuits that compare two binary numbers and determine their relationship (equal, greater than, less than).
Applications of Combinational Circuits
- Combinational circuits are used in various digital systems, including arithmetic units, data processing units, control units, and multiplexers/demultiplexers.
- They are essential building blocks for designing more complex digital systems and processors.
Combinational circuits play a crucial role in digital logic design, providing the basis for processing and manipulating digital data. Understanding their principles, design methods, and applications is essential for anyone working in the field of digital systems and computer engineering.
5.2 Binary Adder-Subtractor
Half-Adder
The design of a Half Adder is an introductory yet fundamental exercise in Digital Logic Design, showcasing how basic logic gates can be used to perform arithmetic operations. A Half Adder is a combinational circuit that adds two single binary digits (bits) and produces a sum and a carry output. It is called a "half" adder because it does not account for carrying inputs from previous operations, a function handled by a Full Adder. Here, we will break down the design process of a Half Adder step by step.

Define the Problem
The objective is to design a circuit that accepts two binary inputs, referred to as a and b, and produces two outputs:
- Sum (s): The result of the addition of a and b.
- Carry (cout): The carry value if the addition of a and b exceeds 1.
Design Steps:
Step 1: Derive the Truth Table
Start by creating a truth table that lists all possible combinations of the input bits a and b, along with the corresponding Sum and Carry outputs.

Step 2: Determine the Logic Expressions
From the truth table, deduce the logic expressions for Sum and Carry. The expressions can be directly inferred based on the outputs:
- Sum (s) can be seen to follow the XOR pattern: s = a ⊕ b
- Carry (cout) follows the AND pattern: cout = a ⋅ b
Step 3: Implement the Circuit Using Logic Gates
Based on the logic expressions derived, you can now draw the circuit:
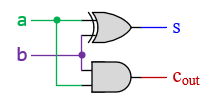
Full-Adder
A 1-bit full-adder is a digital circuit that performs the addition of three binary digits: two significant bits and an incoming carry bit. It's an extension of the half-adder, capable of handling the carry input from a previous addition. The full adder has three inputs: a, b, and Carry-in (cin), and two outputs: Sum (s) and Carry-out (cout). The Sum output represents the least significant bit of the addition of a, b, and cin, while Carry-out represents an overflow into the next most significant bit.
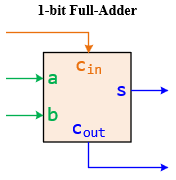
Objectives of a 1-bit Full-Adder:
- Sum (s) Output: The output should be the sum of a, b, and cin modulo 2.
- Carry-out (cout) Output: The output should be 1 if the sum of a, b, and cin is greater than or equal to 2, indicating a carry to the next higher bit.
Design Steps:
Step 1: Derive the Truth Table
Create a truth table that lists all possible combinations of the inputs a, b, and cin, along with the corresponding Sum (s) and Carry-out (cout) outputs.

Step 2: Determine the Logic Expressions
From the truth table, deduce the logic expressions for Sum and Carry-out:
- Sum (s): This can be achieved through the equation: s = a ⊕ b ⊕ cin
- Carry-out (cout): This is a bit more complex, as cout is 1 in three cases: cout = a⋅b + b⋅cin + a⋅cin
Step 3: Implement the Circuit Using Logic Gates
Given the logic expressions, the full-adder circuit can be constructed with:
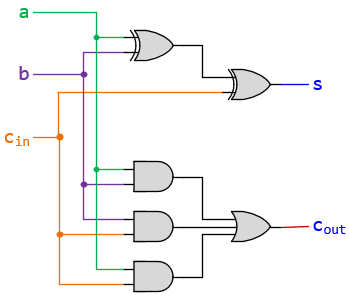
The 1-bit full-adder is essential for constructing arithmetic logic units (ALUs) and multi-bit adders, core components of computer processors and digital systems. Understanding its design and operation is crucial for students and engineers working in digital logic and computer architecture, enabling the creation of more complex computational devices.
Redesigning the 1-bit full adder using fewer gates
Redesigning a 1-bit full-adder to use fewer gates without compromising its functionality requires a clever approach to minimize the hardware while ensuring it still performs the necessary addition of three binary digits (two significant bits and one carry bit). The standard 1-bit full-adder circuit typically uses two XOR gates, two AND gates, and one OR gate. The redesign aims to reduce the total number of gates or to use gates in a more efficient configuration.
Redesigned Full-Adder Using Fewer Gates
Redesigning the 1-bit full adder using a 1-bit half adder
...
Overflow
Overflow
Overflow in digital logic design, particularly in the context of binary adders, is a critical concept to understand. It occurs when the result of an addition operation exceeds the range that can be represented with a given number of bits. Here’s a detailed guide on overflow detection in binary adders:
Understanding Binary Addition
- Binary Numbers: Represented using bits (0 and 1).
- Addition Rules:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 with a carry of 1
Types of Overflow
- Unsigned Overflow: When adding two unsigned numbers exceeds the maximum value represented by the given number of bits.
- Signed Overflow: Occurs when the addition of two signed numbers results in a value that exceeds the representable range for signed numbers.
Overflow in Unsigned Binary Addition
- Detection: When carrying out the most significant bit (MSB) is 1.
- Example: For a 4-bit system (0 to 15 range):
1100 (12) + 0101 (5) = 10001 (17) -> 0001 with carry out = 1 (overflow)
Overflow in Signed Binary Addition
Signed numbers are typically represented using Two's Complement notation.
Two’s Complement:
- Positive Numbers: Same as their binary representation.
- Negative Numbers: Invert all bits and add 1 to the least significant bit (LSB).
Overflow Detection Rules:
- Overflow can be detected by examining the carry into and out of the MSB:
- No Overflow: If carry into the MSB equals carry out of the MSB.
- Overflow: If carry into the MSB does not equal carry out of the MSB.
- Example: For a 4-bit system (-8 to 7 range):
- Adding two positive numbers:
0110 (6) + 0101 (5) = 1011 (-5) -> carry into MSB = 1, carry out = 0 (overflow) - Adding two negative numbers:
1010 (-6) + 1101 (-3) = 0111 (7) -> carry into MSB = 0, carry out = 1 (overflow) - Adding a positive and a negative number (no overflow):
0110 (6) + 1110 (-2) = 0100 (4) -> carry into MSB = 0, carry out = 0 (no overflow)
- Adding two positive numbers:
Practical Implementation in Digital Circuits
Full Adder Circuit: The basic building block for multi-bit binary addition.
- Inputs: Two binary digits (A and B) and a carry-in (C_in).
- Outputs: Sum (S) and carry out (C_out).
- Logic Equations:
S = A ⊕ B ⊕ C_in
C_out = (A · B) + (C_in · (A ⊕ B))
4-bit Adder Example:
- A series of full adders can be cascaded to add multi-bit binary numbers.
- Overflow Detection Logic:
- For unsigned numbers, monitor the carry-out of the MSB.
- For signed numbers, compare the carry into and out of the MSB using an XOR gate:
Overflow = C_in(MSB) ⊕ C_out(MSB)
Summary
- Unsigned Addition Overflow: Detected by carry out of the MSB.
- Signed Addition Overflow: Detected by comparing carry into and carry out of the MSB.
Binary Adder/Subtractor
5.3 Decimal Adder
Decimal Adder
A Decimal Adder (also known as a BCD (Binary-Coded Decimal) Adder) is a digital circuit that adds decimal numbers coded in binary form. Here's a detailed breakdown of how a Decimal Adder works and how to design one:
- Understanding BCD (Binary-Coded Decimal)
- BCD Representation: Each decimal digit (0-9) is represented by a 4-bit binary number.
- Example: 5 in BCD is 0101, and 9 in BCD is 1001.
- Basics of BCD Addition
- When adding two BCD numbers, if the result is a valid BCD number (0000 to 1001), no correction is needed.
- If the result is greater than 1001 (decimal 9), a correction is needed by adding 6 (0110) to the result to skip the invalid binary representations (1010 to 1111).
- Steps to Design a Decimal Adder
Step 1: Add Two BCD Digits- Use a 4-bit binary adder to add the two BCD digits and an optional carry from a previous addition.
- Example:
Add 9 (1001) and 5 (0101).
Binary result: 1001 + 0101 = 1110 (decimal 14, invalid BCD).Step 2: Check for Correction
- Check if the binary result exceeds 1001 (9 in decimal).
- A correction is required if the result is greater than 9 or if there is a carry-out from the binary addition.
- If correction is needed, add 6 (0110) to the result.
- Example:
Initial result: 1110
Add correction: 1110 + 0110 = 1 0100 (20 in decimal, where the '1' is a carry-out for the next BCD digit).
- The final result after correction will be a valid BCD digit and a carry-out if the result exceeds 15 (10000 in binary).
- Designing the Circuit
4.1 Full Adder for BCD Addition
- Use a 4-bit binary adder (e.g., a 7483 4-bit binary full adder).
- Inputs: Two 4-bit BCD digits (A and B) and a carry-in (C_in).
- Use combinational logic to detect invalid BCD results.
Invalid if: (Sum > 9) or (Carry-out from 4-bit adder is 1). - Implement correction by adding 0110 (6) using another 4-bit binary adder.
- 4-bit Binary Adder (e.g., 7483 IC): Adds two 4-bit numbers and produces a sum and a carry-out.
- AND, OR, and NOT Gates: To implement the correction logic.
- Second 4-bit Binary Adder: Add the correction value (6) if needed.
- Example Circuit Design
Inputs- A (A3, A2, A1, A0): First 4-bit BCD digit.
- B (B3, B2, B1, B0): Second 4-bit BCD digit.
- C_in: Carry-in from the previous stage.
- S (S3, S2, S1, S0): 4-bit BCD sum.
- C_out: Carry-out to the next BCD digit.
Circuit Operation
Initial Addition:
Add A and B using the first 4-bit binary adder.
Output: Sum (S3, S2, S1, S0) and Carry-out (C4).
Correction Logic:
Detect if the sum exceeds 9 (S3 AND (S2 OR S1)).
OR (Carry-out from initial addition OR invalid BCD sum).
Correction Addition:
If correction is needed, add 0110 (6) to the initial sum using a second 4-bit binary adder.
Final Sum and Carry:
The output from the second adder provides the final BCD sum.
Carry-out indicates overflow to the next BCD digit.
Summary
- A Decimal Adder ensures the correct addition of BCD digits by checking for and correcting invalid BCD results.
- Use combinational logic to detect necessary corrections and apply them using additional binary addition.
- Practical implementations often use standard binary adders and logic gates to create a robust and efficient decimal addition circuit.
5.4 Binary Multiplier
5.5 Binary Divider
5.6 Combinational Logic Circuit Design
The design procedure for combinational logic circuits starts with the problem specification and comprises the following steps:
- Determine the required number of inputs and outputs from the specifications.
- Derive the truth table for each output based on their relationships to the input.
- Simplify the boolean expression for each output. Use Karnaugh Maps or Boolean algebra.
- Draw a logic diagram that represents the simplified Boolean expression.
- Verify the design by analyzing or simulating the circuit.
5 or more
Design a circuit that has a 3-bit binary input and a single output (Z) specified as follows:
- Z = 0, when the input is less than (5)10
- Z = 1, otherwise
BCD to 7-Segment Decoder
Design a BCD to 7-segment decoder circuit for an seven-segment display that has a 4-bit binary input and seven output (seg-a, -b, -c, -d, -e, -f, and -g) specified by the truth table.
Odd Numbers
Design a circuit that has a 3-bit binary input B2, B1, and B0 (where B2 is MSB and B0 is LSB) and a single output (Z) specified as follows:
- Z = 0, even numbers
- Z = 1, odd numbers 1, 3, 5, 7
Bank Alarm System
A bank wants to install an alarm system with movement sensors. The bank has three sensors (A, B, C).
The alarm will be triggered only when at least two sensors activate simultaneously to prevent false alarms produced by a single sensor activation.
Car Safety Buzzer
Turn On the B(uzzer) whenever the D(oor) is Open OR when the K(ey) is in the Ignition AND the S(eat belt) is NOT Buckled. The logic values for each component are as below:
- 0 : Seat Belt is NOT Buckled
1 : Seat Belt is Buckled - 0 : Key is NOT in the Ignition
1 : Key is in the Ignition - 0 : Door is NOT Open
1 : Door is Open - 0 : Buzzer is OFF
1 : Buzzer is ON
Prime Numbers
Design a circuit that has a 3-bit binary input and a single output (Z) specified as follows:
- Z = 0, non prime number
- Z = 1, prime numbers 2, 3, 5, 7
1-bit Half Adder
The half-adder adds two one-bit binary numbers, A and B. The output is the Sum (S) of the two bits and the Carryout (Cout).
{Cout, S} = A + B
1-bit Full Adder
For a full adder, besides the two inputs bits A and B, the Carry in (Cin) bit is included. The outputs are Sum (S) and Carryout (Cout).
{Cout, S} = A + B + Cin
1-bit Half Subtractor
The half-subtractor subtracts two one-bit binary numbers, A and B. It produces the Difference (D) between the two input binary bits, and also produces an output Borrow (Bout) bit that indicates if one has been borrowed. In the subtraction (A - B), the A is called a Minuend bit, and the B is called a Subtrahend bit.
{Bout, D} = A - B
1-bit Full Subtractor
The half-subtractor has three inputs and two outputs. The inputs are A, B, and Bin, which denote the minuend, subtrahend, and previous borrow, respectively. The outputs are D and Bout, which re[resemt the difference and output borrow, respectively.
{Bout, D} = A - B - Bin
2-bit Comparator
Design a circuit that compares two 2-bit unsigned numbers, (A1, A0) and (B1, B0), providing three outputs such that
- LT = 1, if A1A0 < B1B0
- EQ = 1, if A1A0 = B1B0
- GT = 1, if A1A0 > B1B0
2-bit Multiplier
Design a circuit that multiplies two 2-bit unsigned numbers, (A1, A0) and (B1, B0), providing four outputs P3P2P1P0.
(A1, A0) × (B1, B0) = (P3P2P1P0)