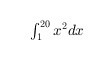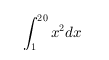Lesson 01: Introduction to MATLAB
What is MATLAB?
The name MATLAB stands for "MATrix LABoratory" and was originally designed as a tool for doing numerical computations with matrices and vectors. It has since grown into a high-performance language for technical computing. MATLAB, integrating computation, visualization, and programming in an easy-to-use environment, allows easy matrix manipulation, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs in other languages. Typical uses include:
- Math and Computation
- Modeling and Simulation
- Data Analysis and Visualization
- Application Development
- Graphical User Interface development
Getting Started
Window Layout
MATLAB development IDE can be launched from the icon created on the desktop. The main working window in MATLAB is called the desktop. When MATLAB is started, the desktop appears in its default layout:
The following tools are managed by MATLAB desktop, although not all of them appear by default when you first start
- Current Folder - This panel allows you to access the project folders and files.
- Command Window - This is the main area where commands can be entered at the command line.It is indicated by the command prompt (>>).
- Workspace - The workspace shows all the variables created and/or imported from files.
- Command History - This panel shows or rerun commands that are entered at the command line.
By default, the Command History window closes after a statement is selected or the Esc key is pressed. To keep the Command History window open, in the Command History window, click and then select either Detach or Dock. If the Command History window is closed while detached or docked, go to the Home tab, and in the Environment section, click Layout. Then, under Show, click Command History and select either Docked or Popup.
1.1 MATLAB Basics
MATLAB Basics
Variables
Variables
MATLAB does not require a command to declare variables. A variable is created simply by directly allocating a value to it. All variables are created with double precision unless specified and they are matrices.
>> v = 3
v =
3
After these statements, the variables are 1x1 matrices with double precision.
>> 23 + 18 # no declarations needed
ans =
41
>> product = 18 * 32.64 # mixed data type
product =
5.875200000000000e+02
>> product = 18 * 555.24; # semi-colon suppresses output of calculation's result
>> product
product =
9.994320000000000e+03
MATLAB Variable Names
- Variable names are CASE SENSITIVE.
- Variable names can contain up to 63 characters (as of MATLAB 6.5 and newer).
- Variable names must start with a letter followed by letters. digits, and underscores ( _ ).
- MATLAB has several keywords that cannot be used as programmer-defined variable names.
The following table provides a list of keywords. The list of keywords can be found by entering the command "iskeyword" on the Command Window.
| break | case | catch | classdef | continue |
| else | elseif | end | for | function |
| global | if | otherwise | parfor | persisyent |
| return | spmd | switch | try | while |
Special Variables and Constants
| Command | Description |
| ans | Temporary variable containing the most recent answer. If you do not assign an output variable to an expression, MATLAB automatically stores the result in ans. |
| eps | This variable name is short for “epsilon”. It is the smallest difference between two numbers that can be represented on the computer. (Smallest incremental number) |
| i, j | The imaginary unit $\sqrt { - 1} $ |
| inf | Infinity. Calculations like n/0, where n is any non-zero real value, result in inf. |
| NaN | Not-a-Number, indicates an undefined numerical result. Expressions like 0/0 and inf/inf result in a NaN, as do arithmetic operations involving a NaN. n/0, where n is complex, also returns NaN. |
| pi | The number $\pi $ ( = 3.1415926535897...) |
| realmin | The smallest usable positive real number. |
| realmax | The largest usable positive real number. |
| computer | Computer type. |
| version | MATLAB version string. |
| clock | This special variable contains the current date and time in the form of a 6-element row vector containing the year, month, day, hour, minute, and second. |
| date | Contains the current data in a character string format, such as 24-Nov-1998. |
Here are several examples that use these values in MATLAB expressions.
>> x = 2 * pi;
>> A = [3+2i 7-8i];
>> tol = 3 * eps;
Matrices and Vectors
Matrices and Vectors
The fundamental unit of data in MATLAB is the array. An array is a collection of data values organized into rows and columns. Arrays can be classified as either vectors, matrices or scalars.
- The term "vector" is usually used to describe an array with only one dimension.
- Row Vector: an array with n elements in a single row (1 x n matrix)
>> a = [1 2 3 4]
a = 1x4
1 2 3 4 - Column Vector: an array with m elements in a single column (m x 1 matrix)
>> b = [1;2;3]
b = 3x1
1
2
3
- Row Vector: an array with n elements in a single row (1 x n matrix)
- The term "matrix" is usually used to describe an array with two or more dimensions.
>> A = [1 , 2 , 3 ; 4, 5, 6]
A =
1 2 3
4 5 6 - A single value, called a Scalars, is represented as a 1 x 1 matrix. A scalar can be created in MATLAB as follows:
>> a_value = 23
a_value =
23
In this text, we will use the term "vector" when discussing one-dimensional arrays and the term "matrix" when discussing arrays with two or more dimensions.
1.2 MATLAB Operators and Special Characters
Arithmetic Operators
Arithmetic Operators
| Symbol | Role |
|---|---|
| + | Addition |
| + | Unary plus |
| - | Subtraction |
| - | Unary minus |
| * | Matrix multiplication |
| / | Matrix right division |
| ^ | Matrix power |
| Symbol | Role |
|---|---|
| .* | Element-wise multiplication |
| .\ | Element-wise left division |
| .^ | Element-wise power |
| .' | Transpose |
| ' | Complex conjugate transpose |
Array Operations
Array Operations
There are two types of arithmetic operators in MATLAB:
- Matrix arithmetic operators, which are governed by the rules of linear algebra.
- Vector arithmetic operators, which are performed element-wise.
Matrix Operations
| Operation | Role Played |
|---|---|
| A + B | Scalar and array addition |
| A - B | Scale and array subtraction |
| A * B | Scale multiplication and multiplication in matrix algebra. (The number of columns in A must equal the number of rows in B.) |
| A / B | Right division: scale division and division in matrix algebra. A / B = A * inv(B) where A and B are matrices |
| A \ B | Left division. A \ B = inv(A) * B, where A and B are matrices. |
| A ^ b | Scalar exponentiation and matrix exponentiation in matrix algebra (Ab) |
| A' | Transpose |
Element-wise Operations
Element-wise Operations
Evaluated element by element
| Operation | Role Played |
|---|---|
| a .* b | Element-by-element multiplication of a and b. Both arrays must be the same shape, or one of them must be a scalar.(dot multiply or dot star). |
| a ./ b | Element-by-element right division of a and b. Both arrays must be the same shape, or one of them must be a scalar. A ./ B = [A(i,j) / B(i,j)], where A and B are arrays [dim(A) = dim(B)] |
| a .\ b | Element-by-element left division of a and b Both arrays must be the same shape, or one of them must be a scalar. A .\ B = [B(i,j) / A(i,j)], where A and B are arrays [dim(A) = dim(B)] |
| a .^ b | Element-wise power. Both arrays must be the same shape, or one of them must be a scalar.(dot power or dot caret). A .^ B = [a(i,j)b(i,j)], for arrays A and B |
| a.' | Array transpose (non-conjugated transpose) |
Example: Array Operations
Give A and B matrices:
A =
1 2 3
4 5 6
7 8 9
B =
3 5 2
5 2 8
3 6 9
Addition
>> X = A + B
X =
4 7 5
9 7 14
10 14 18
Subtraction
>> Y = A - B
Y =
-2 -3 1
-1 3 -2
4 2 0
Product
>> Z = A * B
Z =
22 27 45
55 66 102
88 105 159
Transpose
>> T = A'
T =
1 4 7
2 5 8
3 6 9
Example: Element-Wise Operations
Array operations are very different from matrix operations:
>> A = [1 2; 3 4];
>> B = [5 6; 7 8];
>> A * B
19 22
43 50
But:
>> A .* B
5 12
21 32
The use of "." — "Element" Operation
>> A = [1 2 3 ; 6 2 8 ; 1 4 -2]
A =
1 2 3
6 2 8
1 4 -2
>> x = A(1 , : )
x =
1 2 3
>> y = A( 3 , :)
y =
1 4 -2
>> b = x .* y
b =
1 8 -6
>> c = x ./ y
c =
1.000 0.5000 -1.5000
>> d = x .^ 2
d =
1 4 9
- When you multiply a scalar times an array, you may use either operator ( * or .* ), but they mean something quite different when you multiply two arrays together.
- Unfortunately, when you divide a scalar by an array, you still need to use the ./ syntax because the / means taking the matrix inverse to MATLAB. As a general rule, unless you specifically are doing problems involving linear algebra (matrix mathematics), you should use the dot operators.
Relational Operators
Relational Operators
MATLAB supports six relational operators.
| Operation | Role Played |
| < | Less than |
| <= | Less than or equal to |
| > | Greater than |
| >= | Great than or equal to |
| == | Equal to |
| ~= | Not equal to |
>> A = [2 7 6 ; 9 0 5 ; 3 0.5 6];
>> B = [8 7 0 ; 3 2 5 ; 4 –1 7];
>> A == B
ans =
0 1 0
0 0 1
0 0 0
Logical Operators/Functions
Logical Operators/Functions
MATLAB supports three logical operators.
| Operation | Role Played |
| ~ | logical NOT |
| & | logical AND |
| | | logic OR |
>> u = [1 0 2 3 0 5];
>> v = [5 6 1 0 0 7];
>> u & v
ans =
1 0 1 0 0 1
>> u | v
ans =
1 1 1 1 0 1
>> ~u
ans =
0 1 0 0 1 0
MATLAB also supports some logical functions.
| functions | Role Played |
| xor(A,B) | Logical Exclusive OR. |
| or (A,B) | Logical OR. |
| and (A,B) | Logical AND. |
| not (A) | Logical NOT. |
| any (X) | Returns 1 if any element of X is true or non-zero. any function operates columnwise on matrices. |
| all (X) | Returns 1 if all elements of X are true or non-zero. all operates columnwise on matrices. |
| isnan (X) | Returns 1 at each NaN in X. |
| isinf (X) | Returns 1 at each infinity in X. |
| isfinite (X) | Returns 1 at each finite value in X. |
| isempty (X) | Returns 1 if X is an empty array. An empty array has no elements. |
>> a = 1;
>> b = 1;
>> xor(a, b)
ans =
0
>> A = [0 1 2 ; 3 5 0];
>> all (A)
ans =
0 1 0
>> V = [5 0 8];
>> any (V)
ans =
1
Special Characters
Special Characters
| Symbol | Description |
|---|---|
| @ | Name: At symbol Uses:
Examples: at SymbolCreate a function handle to a named function: fhandle = @myfunct Create a function handle to an anonymous function: fhandle = @(x,y) x.^2 + y.^2; Call the disp method of MySuper from a subclass: disp@MySuper(obj) Call the superclass constructor from a subclass using the object being constructed: obj = obj@MySuper(arg1,arg2,...) |
| . | Name: Period or dot Uses:
3.1415. MATLAB operators that contain a period always work element-wise. The period character also enables you to access the fields in a structure, as well as the properties and methods of an object.Examples: dot SymbolDecimal point: 102.5543 Element-wise operations: A .* B Structure field access: myStruct.f1 Object property specifier: myObj.Property.Name |
| ... | Name: Dot dot dot or ellipsis Uses: Line continuation Three or more periods at the end of a line continue the current command on the next line. If three or more periods occur before the end of a line, then MATLAB ignores the rest of the line and continues to the next line. This effectively makes a comment out of anything on the current line that follows the three periods. Examples: ellipsis SymbolContinue a function call on the next line: sprintf(['The current value '... Break a character vector up on multiple lines and concatenate the lines together: S = ['If three or more periods occur before the '... To comment out one line in a multiline command, use ... at the beginning of the line to ensure that the command remains complete. If you use % to comment out a line it produces an error: y = 1 +... However, this code runs properly since the third line does not produce a gap in the command: y = 1 +... |
| , | Name: Comma Uses: Separator Use commas to separate row elements in an array, array subscripts, function input and output arguments, and commands entered on the same line. Examples: comma SymbolSeparate row elements to create an array: A = [12,13; 14,15] Separate subscripts: A(1,2) Separate input and output arguments in function calls: [Y,I] = max(A,[],2) Separate multiple commands on the same line (showing output): figure, plot(sin(-pi:0.1:pi)), grid on |
| : | Name: Colon Uses:
Examples: colon SymbolCreate a vector: x = 1:10 Create a vector that increments by 3: x = 1:3:19 Reshape a matrix into a column vector: A(:) Assign new elements without changing the shape of an array: A = rand(3,4); Index a range of elements in a particular dimension: A(2:5,3) Index all elements in a particular dimension: A(:,3) for loop bounds: x = 1; |
| ; | Name: Semicolon Uses:
Examples: Semicolon SymbolSeparate rows to create an array: A = [12,13; 14,15] Suppress code output: Y = max(A); Separate multiple commands on a single line (suppressing output): A = 12.5; B = 42.7, C = 1.25; |
| ( ) | Name: Parentheses Uses:
Examples: Parentheses SymbolPrecedence of operations: (A.*(B./C)) - D Function argument enclosure: plot(X,Y,'r*') Indexing: A(3,:) |
| [ ] | Name: Square brackets Uses:
Examples: Square brackets SymbolConstruct a three-element vector: X = [10 12 -3] Add a new bottom row to a matrix: A = rand(3); Create an empty matrix: A = [] Delete a matrix column: A(:,1) = [] Capture three output arguments from a function: [C,iA,iB] = union(A,B) |
| { } | Name: Curly brackets Uses: Cell array assignment and contents Use curly braces to construct a cell array or to access the contents of a particular cell in a cell array. Examples: Curly brackets SymbolTo construct a cell array, enclose all elements of the array in curly braces: C = {[2.6 4.7 3.9], rand(8)*6, 'C. Coolidge'} Index to a specific cell array element by enclosing all indices in curly braces: A = C{4,7,2} |
| % | Name: Percent Uses:
Two percent signs, %%, serve as a cell delimiter as described in Code Sections. Examples: Percent SymbolAdd a comment to a block of code: % The purpose of this loop is to compute Use conversion specifier with sprintf: sprintf('%s = %d', name, value) |
| %{ %} | Name: Percent curly bracket Uses: Block comments The %{ and %} symbols enclose a block of comments that extend beyond one line. Examples: Percent curly bracket SymbolEnclose any multiline comments with percent followed by an opening or closing brace: %{ |
| ! | Name: Exclamation point Uses: Operating system command The exclamation point precedes operating system commands that you want to execute from within MATLAB Not available in MATLAB Online. Examples: Exclamation point SymbolThe exclamation point initiates a shell escape function. Such a function is to be performed directly by the operating system: !rmdir oldtests |
| ? | Name: Question mark Uses: Metaclass for MATLAB class The question mark retrieves the meta.class object for a particular class name. The ? operator works only with a class name, not an object Examples: Question mark SymbolRetrieve the meta.class object for class inputParser: ?inputParser |
| ' ' | Name: Single quotes Uses: Character array constructor Use single quotes to create character vectors that have class char. Examples: Single Quotes SymbolCreate a character vector: chr = 'Hello, world' |
| " " | Name: Double quotes Uses: String constructor Use double quotes to create string scalars that have class string Examples: Double Quotes SymbolCreate a string scalar: S = "Hello, world" |
| Name: Space character Uses: Separator Use the space character to separate row elements in an array constructor, or the values returned by a function. In these contexts, the space character and comma are equivalent. Examples: Space Character SymbolSeparate row elements to create an array: % These statements are equivalent Separate output arguments in function calls: % These statements are equivalent |
|
| enter | Name: Newline character Uses: Separator Use the newline character to separate rows in an array construction statement. In that context, the newline character and semicolon are equivalent. Examples: Newline Character SymbolSeparate rows in an array creation command: % These statements are equivalent |
| ~ | Name: Tilde Uses:
Examples: Tilde SymbolCalculate the logical NOT of a matrix: A = eye(3); Determine where the elements of A are not equal to those of B: A = [1 -1; 0 1] Return only the third output value of union: [~,~,iB] = union(A,B) |
| = | Name: Equal Sign Uses: Assignment Use the equal sign to assign values to a variable. The syntax B = A stores the elements of A in variable B. Examples: Equal Sign SymbolSeparate rows in an array creation command: A = [1 0; -1 0]; The = character is for assignment, whereas the == character is for comparing the elements in two arrays. |
| < & | Name: Left angle bracket and ampersand Uses: Specify superclasses Specify one or more superclasses in a class definition Examples: Left Angle Bracket and Ampersand SymbolDefine a class that derives from one superclass: classdef MyClass < MySuperclass Define a class that derives from multiple superclasses: classdef MyClass < Superclass1 & Superclass2 & … |
| . ? | Name: Dot question mark Uses: Specify fields of name-value structure When using function argument validation, you can define the fields of the name-value structure as the names of all writeable properties of the class. Examples: Equal Sign SymbolSpecify the field names of the propArgs structure as the writeable properties of the matlab.graphics.primitive.Line class. function f(propArgs) |
String and Character Formatting
Some special characters can only be used in the text of a character vector or string. You can use these special characters to insert newlines or carriage returns, specify folder paths, and more.
Use the special characters in this table to specify a folder path using a character vector or string.
| Operation | Role Played |
|---|---|
| / \ |
Name: Slash and Backslash Uses: File or folder path separation In addition to their use as mathematical operators, the slash and backslash characters separate the elements of a path or folder. On Microsoft Windows-based systems, both slash (/) and backslash (\) have the same effect. On The Open Group UNIX-based systems, you must use slash only. Examples: Slash and Backslash SymbolOn a Windows system, you can use either backslash or slash: dir([matlabroot '\toolbox\matlab\elmat\shiftdim.m']) On a UNIX system, use only the forward slash: dir([matlabroot '/toolbox/matlab/elmat/shiftdim.m']) |
| .. | Name: Dot dot Uses: Parent folder Two dots in succession refer to the parent of the current folder. Use this character to specify folder paths relative to the current folder. Examples: Dot Dot SymbolTo go up two levels in the folder tree and down into the test folder, use: cd ..\..\test |
| * | Name: Asterisk Uses: Wildcard character In addition to being the symbol for matrix multiplication, the asterisk * is used as a wildcard character. Wildcards are generally used in file operations that act on multiple files or folders. MATLAB matches all characters in the name exactly except for the wildcard character *, which can match any one or more characters. Examples: Asterisk SymbolLocate all files with names that start with january_ and have a .mat file extension: dir('january_*.mat') |
| @ | Name: At symbol Uses: Class folder indicator An @ sign indicates the name of a class folder. Examples: At Symbol (folder)Refer to a class folder: \@myClass\get.m |
| + | Name: Plus Uses: Package directory indicator A + sign indicates the name of a package folder. Examples: Plus SymbolPackage folders always begin with the + character: +mypack |
1.3 Math Functions
Math Functions
Common Computations
The functions listed in the following table accept either a scalar or a matrix of x values.
| functions | Role Played | MATLAB Example |
| abs (x) | Finds the absolute value of x. | >> abs (-3) ans = 3 |
| sqrt (x) | Finds the square root of x. | >> sqrt (85) ans = 9.2195 |
| nthroot (x,n) | Finds the real nth root of x. This function will not return complex results. | >> nthroot(-2,3) ans = -1.2599 |
| sign (x) | Returns a value:
|
>> sign (-8) ans = -1 |
| rem (x, y) | Computes the remainder of x / y. | >> rem (25, 4) ans = 1 |
| exp (x) | Computes the value of ex, where e is the base for natural logarithms, or approximately 2.7183. | >> exp (10) ans = 2.2026e+04 |
| log (x) | Computes ln(x), the natural logarithm of x (to the base e). | >> log (10) ans = 2.3026 |
| log10 (x) | Computes log10 (x), the common logarithm of x (to the base 10). | >> log10(10) ans = 1 |
Trigonometric Functions
MATLAB includes a complete set of the standard trigonometric functions and the hyperbolic trigonometric functions. Most of these functions assume that angles are expressed in radians.
| functions | Role Played |
| sin (x) | Finds the sine of x when x is expressed in radians, sin(x). |
| cos (x) | Finds the cosine of x when x is expressed in radians, cos(x). |
| tan (x) | Finds the tangent of x when x is expressed in radians, tan(x). |
| asin (x) | Finds the arcsine sin-1(x), or inverse sine, of x, where x must be between -1 and 1. |
| sinh (x) | Finds the hyperbolic sine of x when x is expressed in radians, sinh(x). |
| asinh (x) | Finds the inverse hyperbolic sin of x, sinh-1(x). |
| sind (x) | Finds the sin of x when x is expressed in degrees, sin(xº). |
| asind (x) | Finds the inverse sin of x and reports the result in degrees, sin-1(x). |
1.4 Special Characters
This table lists the supported special characters for the 'tex' interpreter.
| Character Sequence | Symbol | Character Sequence | Symbol | Character Sequence | Symbol |
|---|---|---|---|---|---|
|
|
α |
|
υ |
|
~ |
|
|
∠ |
|
ϕ |
|
≤ |
|
|
|
|
χ |
|
∞ |
|
|
β |
|
ψ |
|
♣ |
|
|
γ |
|
ω |
|
♦ |
|
|
δ |
|
Γ |
|
♥ |
|
|
ϵ |
|
Δ |
|
♠ |
|
|
ζ |
|
Θ |
|
↔ |
|
|
η |
|
Λ |
|
← |
|
|
θ |
|
Ξ |
|
⇐ |
|
|
ϑ |
|
Π |
|
↑ |
|
|
ι |
|
Σ |
|
→ |
|
|
κ |
|
ϒ |
|
⇒ |
|
|
λ |
|
Φ |
|
↓ |
|
|
µ |
|
Ψ |
|
º |
|
|
ν |
|
Ω |
|
± |
|
|
ξ |
|
∀ |
|
≥ |
|
|
π |
|
∃ |
|
∝ |
|
|
ρ |
|
∍ |
|
∂ |
|
|
σ |
|
≅ |
|
• |
|
|
ς |
|
≈ |
|
÷ |
|
|
τ |
|
ℜ |
|
≠ |
|
|
≡ |
|
⊕ |
|
ℵ |
|
|
ℑ |
|
∪ |
|
℘ |
|
|
⊗ |
|
⊆ |
|
∅ |
|
|
∩ |
|
∈ |
|
⊇ |
|
|
⊃ |
|
⌈ |
|
⊂ |
|
|
∫ |
|
· |
|
ο |
|
|
⌋ |
|
¬ |
|
∇ |
|
|
⌊ |
|
x |
|
... |
|
|
⊥ |
|
√ |
|
´ |
|
|
∧ |
|
ϖ |
|
∅ |
|
|
⌉ |
|
〉 |
|
| |
|
|
∨ |
|
〈 |
|
© |
LaTeX Markup
To use LaTeX markup, set the interpreter to 'latex'. For inline mode, surround the markup with single dollar signs ($). For display mode, surround the markup with double dollar signs ($$).
| LaTeX Mode | Example | Result |
|---|---|---|
| Inline |
'$\int_1^{20} x^2 dx$'
|
|
| Display |
'$$\int_1^{20} x^2 dx$$'
|
|
The displayed text uses the default LaTeX font style. The FontName, FontWeight, and FontAngle properties do not have an effect. To change the font style, use LaTeX markup.
The maximum text size you can use with the LaTeX interpreter is 1200 characters. About 10 characters per line reduce multiline text.
Practice Exercises
Exe 1: MATLAB Expressions
Suppose that a = 1 and b = 3. Evaluate the following expressions using MATLAB.
- $\frac{{4a}}{{3b}}$
- $\frac{{2{b^{ - 2}}}}{{{{(a + b)}^2}}}$
- $\frac{{{b^3}}}{{{b^3} - {a^3}}}$
- $\frac{4}{3}\pi {b^2}$
- $\frac{{\inf }}{0}$
- $\sqrt {{a^2} + {b^2}} $
Exe 2: ans Variable
Typing the following MATLAB statements into the Command Window:
4 * 5
a = ans * pi
b = ans / pi
ans
- What are the results in a, b, and ans?
- What is the final value saved in ans?
- Why was that value retained during the subsequent calculations?
Exe 3: Operators
As you perform the following calculations, recall the difference between the * and .* operators, as well as the / and ./ and the ^ and .^ operators:
- Define the matrix a = [2.3 5.8 9] as a MATLAB variable.
- Find the sine of a.
- Add 3 to every element in a.
- Define the matrix b = [5.2 3.14 2] as a MATLAB variable.
- Add together each element in matrix a and in matrix b.
- Multiply each element in a by the corresponding element in b.
- Square each element in matrix a.
- Create a matrix named c of evenly spaced values from 0 to 10, with an increment of 1.
- Create a matrix named d of evenly spaced values from 0 to 10, with an increment of 2.
- Use the linspace function to create a matrix of six evenly spaced values from 10 to 20.
- Use the logspace function to create a matrix of five logarithmically spaced values between 10 and 100.
Exe 4: Math Function
Calculate the following (remember that mathematical notation is not necessarily the same as MATLAB notation):
- $\sin (2\theta )$ for $\theta = 3\pi $
- $\cos (\theta )$ for $0 \le \theta \le 2\pi $ ; let $\theta $ change in steps of $0.2\pi $
- ${\sin ^{ - 1}}(1)$
- ${\cos ^{ - 1}}(x)$ for $ - 1 \le x \le 1$ ; let x change in steps of 0.2.
- Find the cosine of 45º.
- Convert the angle from degrees to radians, and then use cos function.
- Use the cosd function.
- Find the angle whose sine is 0.5. Is your answer in degrees or radians?
- Find the cosecant of 60. You may have to use the help function to find the appropriate syntax.
Exe 5: Valid MATLAB variable names
Which are valid variable names?
- r2d2
- name$
- _2a
- pay_day
- 2a
- y____5
- switch