Lesson 06: User-Controlled Input and Output
Objective
- Learn how to prompt the user for input to a script
- Learn how to create output with the disp function
- Learn how to create tables using the table function
- Learn how to create formatted output using fprintf
- Learn how to create formatted output for use in other function with the sprintf function
Background
The simplest type of MATLAB program is called a script. A script is a file that contains multiple sequential lines of MATLAB commands and function calls. You can run a script by typing its name at the command line.
There are two ways to create a script file
- Click New Script icon to create a new script file
- Or, in the command windows, use the edit command
>> edit myScriptName
This command opens a blank file named myScriptName.m in the current workspace folder.
To run the script, type its name at the command line:
>> myScriptName
In this lab, you have to implement the code using Script file.
6.1 Inputs
| Syntax | Description |
|---|---|
| x = input(prompt) | Displays the text in prompt and waits for the user to input a value and press the [Return] key. The user can enter expression, like pi/3 or rand(3), and can be variables in the workspace.
|
| str = input(prompt,'s') | Returns the entered text, without evaluating the input as an expression. |
The text string for the prompt may contain one or more special format commands.
| Format Command | Resulting Action |
|---|---|
| '' | Single quotation mark |
| %% | Percent character |
| \\ | Backslash |
| \a | Alarm |
| \b | Backspace |
| \f | Form feed |
| \n | New line |
| \r | Carriage return |
| \t | Horizontal tab |
| \v | Vertical tab |
| \xN |
Character whose Unicode numeric value can be represented by the hexadecimal number, N Example: sprintf('\x5A') returns 'Z' |
| \N | Character whose Unicode numeric value can be represented by the octal number, N Example: sprintf('\123') returns 'Z' |
Request Numeric Input or Expression
Request a numeric input, and then multiply the input by 10.
prompt = 'Enter a value: ';
x = input(prompt)
y = x * 10
At the prompt, enter a numeric value or array, such as 32.
x = 32
y = 320
The input function also accepts expressions. For example, return the code.
prompt = 'Enter a value: ';
x = input(prompt)
y = x * 10
At the prompt, enter magic(3).
x =
8 1 6
3 5 7
4 9 2
y =
80 10 60
30 50 70
40 90 20
Request String Input with Single Quotes
Data entered with input does not need to be numeric information. For example, we prompt the user with the following command:
x = input('Enter your name in single quotes')
At the prompt, enter 'Ryan Lin'
x = 1 × 8 9 Bytes Char
Ryan Lin
If you are entering a string, you must enclose the characters in single quotes.
Request String Input without Quotes
Input a string
x = input('Enter your name:', 's')
Now, you need only enter the characters, such as
Ryan Lin
and the program responds with
x = 1 × 8 9 Bytes Char
Ryan Lin
Request Unprocessed Text Input
Request a simple text response that requires no evaluation.
prompt = 'Do you want more? Y/N [Y]: ';
str = input(prompt,'s');
if isempty(str)
str = 'Y';
end
The input function returns the text exactly as typed. If the input is empty, this code assigns a default value, 'Y', to str.
Prompt Text with Variables
Use two input lines to ask the user to input the name of the 'planet', then the next question asks the mass of the planet.
name = input('What is the name of the exoplanet?', 's');
massPlanet = input( sprintf('What is the estimated mass of %s (kg)?', name), 's');
Practice Exercises 6.1
- Calculate the area A of a triangle:
$A = {1 \over 2}base \times height$
Prompt the user to enter the values for the base and for the height. - Create a vector from 0 to n, allowing the user to enter the value of n.
- Create a vector that starts at a, ends at b, and has a spacing of c. Allow the user to input all of these parameters.
6.2 Outputs
There are three common ways to print (output) in MATLAB:
- Type the name of a variable without a trailing semi-colon.
- Use the disp function
- Use the fprintf function, which accepts a C printf-style formatting string.
Here are examples:
>> x = [1 2 3 4];
>> x
x = 1 2 3 4
>> disp(x)
1 2 3 4
>> fprintf('%i\n',x)
1
2
3
4
Display Function
Display Function
| Syntax | Description |
|---|---|
| disp(X) | Displays the value of variable X without printing the variable name. If a variable contains an empty array, disp returns without displaying anything. |
Display Variable Values
Create a variable with numbers and another variable with text.
A = [15 150];
S = 'Hello World!';
disp(A)
disp(S)
MATLAB returns
15 150
Hello World
Display Matrix with Column Labels
Display a matrix and label the columns as Corn, Oats, and Hay.
x = rand(2,3);
disp(' Corn Oats Hay')
disp(x)
MATLAB responds
Corn Oats Hay
0.8147 0.0975 0.1576
0.1270 0.2785 0.9706
Display Hyperlink in Command Window
Display Multiple Variables on Same Line
Here are three ways to displays variable values on the same line in the Command Window.
-
Concatenate multiple character vectors together using the [] operator. Convert any numeric values to characters using the num2str function. Use disp to display the result.
name = 'Kevin';
age = 12;
X = [name, ' will be ', num2str(age), ' this year.'];
disp(X)Kevin will be 12 this year.
-
Use sprintf to create text, and then display it with disp.
name = 'Kevin';
age = 12;
X = sprintf('%s will be %d this year.', name. age);
disp(X)Kevin will be 12 this year.
-
Use fprintf to directly display the text without creating a variable. However, to terminate the display property, you must end the text with the newline (\n) meta-character.
name = 'Ryan';
age = 14;
fprintf('%s will be %d this year.\n', name, age);Ryan will be 14 this year.
Formatted Output - The fprintf Function
| Syntax | Description |
|---|---|
| fprintf(text) fprintf(formatSpec, var, ...) |
The fprintf command displays formatted text and can display formatSpec along with the contents of var. |
| nbyte = fprintf(__) | Return the number of bytes that fprintf writes. |
formatSpec can be a character vector in single quotes, or a string scalar.
The fprintf function provides more control over the output than the disp function. In addition to displaying the values, and matrix values, you can specify the format to be used in displaying the values, and you can specify when to skip to a new line.
Print Literal Text and Array Values
Print multiple numeric values and literal text to the screen.
A1 = [9.9, 9900];
A2 = [8.8, 7.7 ; ...
8800, 7700];
formatSpec = 'X is %4.2f meters or %8.3f mm\n';
fprintf(formatSpec, A1, A2)
X is 9.90 meters or 9900.000 mm
X is 8.80 meters or 8800.000 mm
X is 7.70 meters or 7700.000 mm
- %4.2f in the formatSpec input specifies that the first value in each line of output is a floating-point number with a field width of four digits, including two digits after the decimal point.
- %8.3f in the formatSpec input specifies that the second value in each line of output is a floating-point number with a field width of eight digits, including three digits after the decimal point.
- \n is a control character that starts a new line.
Print Double-Precision Values as Integers
Explicitly convert double-precision values with fractions to integer values.
a = [1.02 3.04 5.06];
fprintf('%d\n',round(a));
1
3
5
- %d in the formatSpec input prints each value in the vector, round(a), as a signed integer.
- \n is a control character that starts a new line.
Print a Two Arrays into a Table Format
Display a table that convert inches to feet.
clear all; close all; clc;
disp('Inches to Feet Convertsion Table')
disp(' Inches Feet')
inches = 0:10:120;
feet = inches ./ 12;
results = [inches; feet];
fprintf(' %8.0f %8.2f \n', results)
Inches to Feet Convertsion Table
Inches Feet
0 0.00
10 0.83
20 1.67
30 2.50
40 3.33
50 4.17
60 5.00
70 5.83
80 6.67
90 7.50
100 8.33
110 9.17
120 10.00
Display Hyperlinks in Command Window
Display a hyperlink (The MathWorks Web Site) on the screen.
url = 'http://www.AirSupplyLab.com';
sitename = 'The Air SUpply Lab Web Site';
fprintf('<a href = "%s">%s</a>\n',url, sitename)
%s in the formatSpec input indicates that the values of the variables url and sitename, should be printed as text.
Formatted Output - The sprintf Function
| Syntax | Description |
|---|---|
| str = sprintf(formatSpec, A1, ... , An) | Formats the data in arrays A1,...,An using the formatting operators specified by formatSpec and returns the resulting text in str. The sprintf function formats the values in A1,...,An in column order. If formatSpec is a string, then so is the output str. Otherwise, str is a character vector. To return multiple pieces of formatted text as a string array or a cell array of character vectors, use the compose function. |
| [str,errmsg] = sprintf(formatSpec, A1, ... , An) | Returns an error message as a character vector when the operation is unsuccessful. Otherwise, errmsg is empty. |
| str = sprintf(literalText) | Translates escape-character sequences in literalText, such as \n and \t. It returns all other characters unaltered. If literalText contain a formatting operator (such as %f), then str discards it and all characters after. |
Floating-Point Formats
Format a floating-point number using %e, %f, and %g specifiers.
A = 1/eps;
str_e = sprintf('%0.5e',A)
str_e = '4.50360e+15'
str_f = sprintf('%0.5f',A)
str_f = '4503599627370496.00000'
str_g = sprintf('%0.5g',A)
str_g = '4.5036e+15'
Literal Text and Array Inputs
Combine literal text with array values to create a character vector.
formatSpec = 'The array is %dx%d.';
A1 = 2;
A2 = 3;
str = sprintf(formatSpec, A1, A2)
str = 'The array is 2x3.'
Specify Formatted Text as String Array
To return formatted text as a string, specify formatSpec as a string instead of a character vector when you call the sprintf function.
Starting in R2017a, you can create strings using double quotes. Convert data and return the result as a string.
formatSpec = "The current time is: %d:%d %s";
A1 = 11;
A2 = 20;
A3 = 'a.m.';
str = sprintf(formatSpec, A1, A2, A3)
str = "The current time is: 11:20 a.m."
Convert input string. Input arrays that contain text either can be character vectors or strings.
A1 = 2;
A2 = 35;
A3 = "p.m.";
str = sprintf(formatSpec, A1, A2, A3)
str = "The current time is: 2:35 p.m."
Integer Format with Floating-Point Inputs
Explicitly convert double-precision values to integers.
str = sprintf('%d',round(pi))
str = '3'
Specify Field Width of a Printed Value
Specify the minimum width of the printed value.
str = sprintf('%025d',[123456])
str = '0000000000000000000123456'
The 0 flag in the %025d format specifier requests leading zeros in the output.
Reorder Inputs Using Position Identifier (n$)
Reorder the input values using the n$ position identifier.
A1 = 'X';
A2 = 'Y';
A3 = 'Z';
formatSpec = ' %3$s %2$s %1$s';
str = sprintf(formatSpec, A1, A2, A3)
str = 'Z Y X'
Create Character Vector from Values in Cell Array
C = { 1, 2, 3 ;
'AA','BB','CC'};
str = sprintf(' %d %s',C{:})
str = ' 1 AA 2 BB 3 CC'
The syntax C{:} creates a comma-separated list of arrays that contain the contents of each cell from C in column order. For example, C{1}==1 and C{2}=='AA'.
The table Function
table arrays store column-oriented or tabular data, such as columns from a text file or spreadsheet. Tables store each piece of column-oriented data in a variable. Table variables can have different data types and sizes as long as all variables have the same number of rows. Use the summary function to get information about a table.
To index into a table, use smooth parentheses () to return a subtable or curly braces {} to extract the contents. You can reference variables and rows using names.
| Syntax | Description |
|---|---|
| T = table(var1, ... ,varN) | Creates a table from the input variables var1,...,varN. Variables can be of different sizes and data types, but all variables must have the same number of rows. |
| T = table('Size',sz,'VariableTypes',varType) | Creates a table and preallocates space for the variables that have data types you specify. sz is a two-element numeric array, where sz[1] specifies the number of rows and sz[2] specifies the number of variables. varTypes is a cell array of character vectors specifying data types. |
| T = table(___,'VariableNames',varNames) | Specifies the names of the variables in the output table. You can use this syntax with the input arguments from any of the other syntaxes for this function. |
| T = table(___,'RowNames',rowNames) | Specifies names of the rows in the output table. You can use this syntax with the input arguments of any of the previous syntaxes. |
| T = table | Creates an empty 0×0 table. |
Specify Variable Names
Create a table from arrays. To specify table variable names, use the 'VariableNames' name-value pair argument.
g = [9.8;1.6];
d = 0.5 * g * 100 ^2;
p = {'Earth';'Moon'};
table(p, g, d, 'VariableNames',{'Planet','g','Distance'})
ans = 2×3 table
Planet g distance
_______ ___ ________
'Earth' 9.8 49000
'Moon' 1.6 8000
Create a table with the state names as row names. You can specify both the 'VariableNames' and 'RowNames' name-value pairs when using the table function.
table(p, g, d, 'VariableNames',{'Planet','g','Distance'},'RowNames',{'#1';'#2'})
ans = 2×3 table
Planet g Distance
_______ ___ ________
#1 'Earth' 9.8 49000
#2 'Moon' 1.6 8000
Specify Size and Variable Types
Preallocate a table by specifying its size and the data types of the variables. The table function fills the variables with default values that are appropriate for the data types you specify. It also gives the variables default names, but you also can assign variable names of your own. Preallocation provides room for data you add to the table later.
sz = [4 3];
varTypes = {'double','datetime','string'};
T = table('Size',sz,'VariableTypes',varTypes)
T = 4×3 table
Var1 Var2 Var3
____ ____ _________
0 NaT <missing>
0 NaT <missing>
0 NaT <missing>
0 NaT <missing>
To specify names for the variables, use the 'VariableNames' name-value pair argument.
varNames = {'Temperature','Time','Station'};
T2 = table('Size',sz,'VariableTypes',varTypes,'VariableNames',varNames)
T2 = 4×3 table
Temperature Time Station
___________ ____ _________
0 NaT <missing>
0 NaT <missing>
0 NaT <missing>
0 NaT <missing>
Add rows of data to the first two rows of T2. Preallocation can be a useful technique when your code adds one row of data, or a few rows of data, at a time. Instead of growing the table every time you add a row, you can fill in table variables that already have room for your data.
T2(1,:) = {75,datetime('now'),"S1"};
T2(2,:) = {68,datetime('now')+1,"S2"}
T2 = 4×3 table
Temperature Time Station
___________ ____________________ _________
75 21-Feb-2019 20:47:46 "S1"
68 22-Feb-2019 20:47:46 "S2"
0 NaT <missing>
0 NaT <missing>
You can encapsulate a row of data values in a cell array. When you assign a row from a cell array, elements from the cell array are assigned to the row in the table.
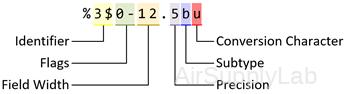
Formatting Operator
A formatting operator starts with a percent sign, %, and ends with a conversion character. The conversion character is required. Optionally, you can specify identifier, flags, field width, precision, and subtype operators between % and the conversion character. (Spaces are invalid between operators and are shown here only for readability).
Conversion Character
This table shows conversion characters to format numeric and character data as text.
| Value Type | Conversion | Details |
|---|---|---|
| integer, singed | %d or %i | Base 10 |
| integer, unsigned | %u | Base 10 |
| %o | Base 8 (Octal) | |
| %x | Base 16 (Hexadecimal), lowercase letters a ~ f | |
| %X | Same as %x, uppercase letters A ~ F | |
| floating-point number | %f | Fixed-point notation (Use a precision operator to specify the number of digits after the decimal point.) |
| %e | Exponential notation, such as 3.141593e+00 (Use a precision operator to specify the number of digits after the decimal point.) | |
| %E | Same as %e, but uppercase, such as 3.141593E+00 (Use a precision operator to specify the number of digits after the decimal point.) | |
| %g | The more compact of %e or %f, with no trailing zeros (Use a precision operator to specify the number of significant digits.) | |
| %G | The more compact of %E or %f, with no trailing zeros (Use a precision operator to specify the number of significant digits.) | |
| characters or strings | %c | Single character (displays one character at a time) |
| %s | Character vector or string array (displays the entire string). The type of the output text is the same as the type of formatSpec. |
Optional Operators
The optional identifier, flags, field width, precision, and subtype operators further define the format of the output text.
- Identifier
Order for processing the function input arguments. Use the syntax n$, where n represents the positions of the other input arguments in the function call.
Example: ('%3$s %2$s %1$s %2$s','A','B','C') prints input arguments 'A', 'B', 'C' as follows: C B A B.
Note: If an input argument is an array, you cannot use identifiers to specify particular array elements from that input argument. - Flags
'-' Left-justify
Example: %-5.2f
Example: %-10s'+' Always print a sign character (+ or -) for any numeric value. ' ' Insert a space before the value.
Example: % 5.2f'0' Pad to field width with zero before the value.
Example: %05.2f'#' Modify selected numeric conversions:
- For %o, %x, or %X, print 0, 0x, or 0X prefix.
- For %f, %e, or %E, print decimal point even when precision is 0.
- For %g or %G, do not remove trailing zeros or decimal point.
- Field Width
Minimum number of characters to print. The field width operator can be a number, or an asterisk (*) to refer to an input argument.
When you specify * as the field width operator, the other input arguments must provide both a width and a value to be printed. Widths and values can be pairs of arguments or pairs within a numeric array. With * as the field width operator, you can print different values with different widths.
Example: The input arguments ('%12d',intmax) are equivalent to ('%*d',12,intmax).
Example: The input arguments ('%*d',[2 10 5 100]) return '10 100', with two spaces allocated for 10 and five spaces for 100. As an alternative, you also can specify the field widths and values as multiple arguments, as in ('%*d',2,10,5,100). The function pads to field width with spaces before the value unless otherwise specified by flags.
- Precision
For %f, %e or %E Number of digits to the right of the decimal point
Example: '%.4f' prints pi as '3.1416'For %g or %G Number of significant digits
Example: '%.4g' prints pi as '3.142'The precision operator can be a number, or an asterisk (*) to refer to an argument.
- When you specify * as the field precision operator, the other input arguments must provide both a precision and a value to be printed. Precisions and values can be pairs of arguments, or pairs within a numeric array. With * as the precision operator, you can print different values to different precisions.
- When you specify *.* as field width and precision operators, you must specify field widths, precisions, and values as triplets.
- Example: The input arguments ('%.4f',pi) are equivalent to ('%.*f',4,pi).
- Example: The input arguments ('%6.4f',pi) are equivalent to ('%.*f',6,4,pi).
- Example: The input arguments ('%*.*f',6,4,pi,9,6,exp(1)) return '3.1416 2.718282', with 9 and 6 as the field width and precision for the output of exp(1).
- Subtype:
You can use a subtype operator to print a floating-point value as its octal, decimal, or hexadecimal value. The subtype operator immediately precedes the conversion character. This table shows the conversions that can use subtypes.Floating-point numberInput Value Type Subtype and Conversion Character Output Value Type Floating-point number %bx or %bX
%bo
%buDouble-precision hexadecimal, octal, or decimal value
Example: %bx prints pi as 400921fb54442d18%tx or %tX
%to
%tuSingle-precision hexadecimal, octal, or decimal value
Example: %tx prints pi as 40490fdb
Practice Exercises 6.2
- Use two separate input statements to prompt a user to enter his or her first and last names. Use the disp function to display those names on one line.
- Prompt the user to enter an array of numbers. Use the length function to determine how many values were entered, and use disp function to report your results to the command Window.
- Repeat Exercise 2, and use fprintf to report your results.
- Use fprintf to create the multiplication tables from 1 to 13 for the number 6. Your table should look like this:
1 times 6 is 6
2 times 6 is 12
3 times 6 is 18
.
. - Consider the patient data contained in the following table:
Patient Last Name Patient First Name Age Height (inches) Weight (lb) Smith Fred 6 47 82 Jones Kathy 22 66 140 Webb Milton 92 62 110 Anderson John 45 72 190 - Create a column vector of last names called last, using curly braces.
- Create a column vector of first names, called first, using curly braces.
- Create column vectors for age, height and weight.
- Display the information using table function.
6.3 Graphic Input
| Syntax | Description |
|---|---|
| [x,y] = ginput(n) | Allows you to identify the coordinates of n points. To choose a point, move your cursor to the desired location and press either a mouse button or a key on the keyboard. Press the [Return] key to stop before all n points are selected. |
| [x,y] = ginput | Allows you to select an unlimited number of points until you press the [Return] key. |
| [x,y,button] = ginput(__) | Also returns the mouse button or key on the keyboard used to select each point. |
Identify Points and Plot Coordinates
Identify four points in a set of axes using ginput. To select each point, move the cursor to your desired location and press a mouse button or key.
>> [x,y] = ginput(4)
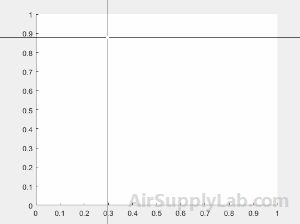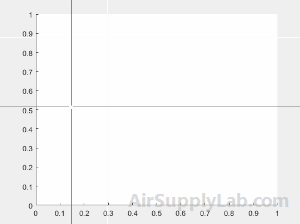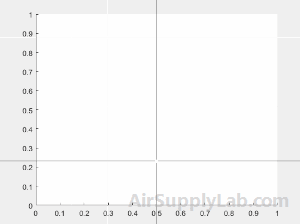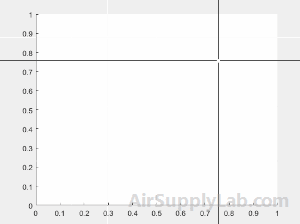
x =
0.2984
0.1463
0.5012
0.7569
y =
0.8790
0.5146
0.2318
0.7566
Plot the points:
>> plot(x,y)
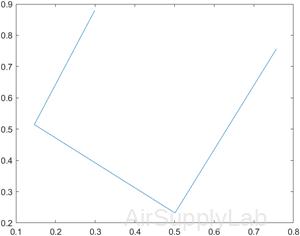
Pick Points Off a Graph
Create a graphic:
x = 5:30;
y = x.^2 - 40*x + 400;
plot(x,y)
axis([5, 30, -50, 250])
[a, b] = ginput
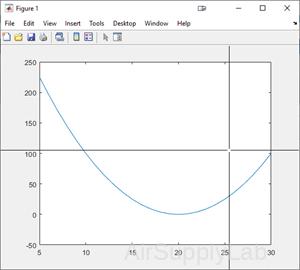
a = 25.4781
b = 105.2478
Practice Exercises 6.4
- At time $t = 0$, when a rocket's engine shuts down, the rocket has reached an altitude of 500 m and is rising at a velocity of 125 m/s. At this point, gravity takes over. The height of the rocket as a function of time is
$h(t) = - {{9.8} \over 2}{t^2} + 125t + 500$ for $t>0$
Plot the height of the rocket from 0 to 30 seconds, and- Use the ginput function to estimate the maximum height the rocket reaches and the time when the rocket hits the ground.
- Use the disp command to report your results to the command window.
6.4 Section Dividers
6.5 File Access
Questions
- This problem requires you to generate temperature conversion tables. Use the following equations, which describe the relationships between temperatures in degrees Fahrenheit (TF), degrees Celsius (TC), kelvins (TK), and degrees Rankine (TR), respectively:
$${T_F} = {T_R} - 459.67^\circ R$$
$${T_F} = {9 \over 5}{T_C} + 32^\circ F$$
$${T_R} = {9 \over 5}{T_K}$$
You will need to rearrange these expressions to solve some of the problems.- Generate a table of conversions from Fahrenheit to Kelvin for values from 0°F to 200°F. Allow the user to enter the increments in degrees F between lines. Use disp and fprintf to create a table with a title, column headings, and appropriate spacing.
- Generate a table of conversions from Celsius to Rankine. Allow the user to enter the starting temperature and the increment between lines. Print 25 lines in the table. Use disp and fprintf to create a table with a title, column headings, and appropriate spacing.
- Generate a table of conversions from Celsius to Fahrenheit. Allow the user to enter the starting temperature, the increment between lines, and the number of lines for the table. Use disp and fprintf to create a table with a title, column headings, and appropriate spacing.